Ecuaciones y sistemas de ecuaciones

Ecuaciones de segundo grado

En esta página resolvemos 15 problemas sobre ecuaciones de segundo grado. En la mayoría de los problemas se pide calcular las soluciones de las ecuaciones. Las últimas 4 ecuaciones tienen soluciones complejas.

Recordatorio

La forma general de una ecuación de segundo grado es:

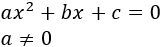
Por comodidad, resolveremos la ecuación de tres formas distintas según los valores de los coeficientes $b$ y $c$.

Se llama discriminante, $\Delta$, a

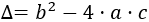
El signo de $\Delta$ nos permite conocer el tipo de soluciones de la ecuación:

• Si $\Delta >0$, hay dos soluciones reales distintas.
• Si $\Delta =0$, hay dos soluciones reales iguales.
• Si $\Delta <0$, no hay soluciones reales (hay dos soluciones complejas distintas).

Caso 1

Si $b$, $c\ne 0$, se dice que la ecuación es completa y sus soluciones las proporciona la fórmula

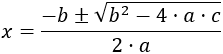
La ecuación está escrita en la forma general y su discriminaste es

$$\Delta =b^2-4ac=$$

$$=(-2{)}^2-4\cdot 1\cdot (-1)=$$

$$=4+4=8$$

Como Δ > 0, existen dos raíces y son simples.

Calculamos las raíces:

$$x=\frac{2\pm \sqrt{8}}{2}=$$

$$=\frac{2\pm 2\sqrt{2}}{2}=$$

$$=1\pm \sqrt{2}$$

Por tanto, tenemos las soluciones :

$$x=1+\sqrt{2},1-\sqrt{2}$$

Una factorización de la ecuación es

$$(x-1-\sqrt{2})(x-1+\sqrt{2})=0$$

•TEOREMA DEL RESTO

•El resto  de la división de un polinomio P(x) entre un binomio de la forma (x ‑ a) , es el valor del polinomio al sustituir la variable x por el valor de a.

•Si el binomio es de la forma (x + a) , sustituiremos la  x  por  ‑ a.

•

•TEOREMA DEL FACTOR

•Si el resto  de la división de un polinomio P(x) entre un binomio de la forma (x ‑ a) , es cero, el binomio (x – a) es un factor de P(x).

•

•P(x) = (x – a).Q(x)

•

•Además, si el resto es cero, la división es exacta y el valor de a se dice que es un cero o una raíz del polinomio.

•Si un polinomio es de grado n , tendrá como máximo n raíces reales.

•Si un polinomio es de grado impar tendrá obligatoria-mente una raíz real.

•Si es de grado par tendrá 0, 2, 4 , … raíces reales.

ejemplos de teorema del resto.

•Ya hemos visto al hacer la división por Ruffini:

•( x3  + 4.x2  -  5 ) : ( x  - 3 ),  que el resto  es 58

•

•Veamos aplicando el Teorema del resto:

•P(a)=P(3)= 33  + 4.32  -  5 = 27 + 36 – 5 = 58

•

•Ya hemos visto al hacer la división por Ruffini:

•( x3  + 4.x2  -  5 ) : ( x  + 5 ),  que el resto es – 30

•

•Veamos aplicando el Teorema del resto:

•P(a)=P(-5)= (-5)3  + 4.(-5)2  -  5 = -125 + 100 – 5 = - 30

•

•Ya hemos visto al hacer la división por Ruffini:

•( 4.x3  + 5.x  -  3 ) : ( x  + 2 ),   que el resto es – 45

•

•Veamos aplicando el Teorema del resto:

•P(a)=P(-2)= 4.(-2)3  + 5.(-2)  - 3 = - 32 – 10 – 3 = - 45

La practica esta en este enlace, sigue los pasos para descargar la practica.

Practica de Reposición para el P1